The model

Same as in the previous post, repeated here for easy reference.

$$ \frac{d\psi_\pm}{dt} = \left[\frac{1}{2}(Rn_\pm - \gamma) - \frac{i}{\hbar}\left(E_\pm + \alpha_\pm|\psi_\pm|^2 + \beta_\pm|\psi_\mp|^2 + K_\pm\left(n_\mp + \frac{\mathcal{P}_\mp}{W}\right) + G_\pm\left(n_\pm + \frac{\mathcal{P}_\pm}{W}\right)\right)\right]\psi_\pm - \frac{iE_{XY}}{2\hbar}\psi_\mp $$ $$ \frac{dn_\pm}{dt} = -(\Gamma + \Gamma_{s,\pm} + R|\psi_{\pm}|^2)n_\pm + \Gamma_{s,\mp}n_\mp + \mathcal{P}_{\pm} $$

I had some difficulties with this model, so here I'm going to progressively add complexity to the more basic model and see where/if things start to break down.

The simulations use $E_0=1.9$, $\Delta t = 0.05$, $\Omega_0 = 4$, $\gamma = 0.181818\ldots$, $\gamma_{dia}=0.117$, $g_X = -0.364$, $\xi = 47$, $\Gamma = 0.05$, $\eta_1 = 0.0002$, $u_X = 0.01$, $R = 0.012$, $EXY = 0.0002$, using units of meV, µm, ps, and T. The pumping power range used in all these graphs is the same, the label $P/P_{th}$ may not be accurate for all graphs. At the lower end, $P=P_0 = 1.65$ and $\mathcal{P}_\pm$ is calculated the same way as in the original paper. At the higher end, $P= 4.5P_0$.

The simulation is run for 600.000 steps initially to let it settle into some kind of stable solution, I then take 256 samples of $\psi_-^*\psi_+$ at 300 step intervals of the same size.

$\beta_\pm = 0$ and $K_\pm = 0$

Using a model that incorporates $\beta_\pm$ and $K_\pm$ but no magnetic field dependent correction and setting them to 0, and also calculating $B_{int}$: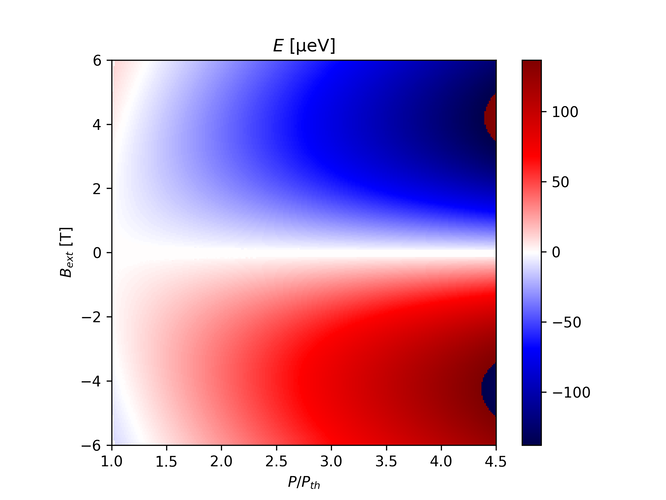

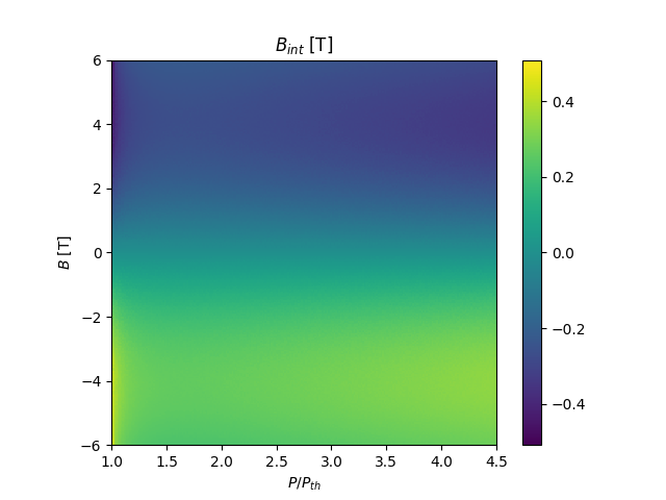
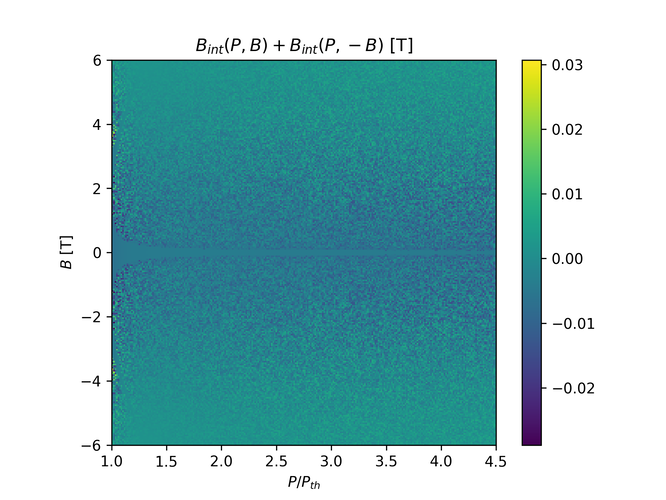
We expect $B_{int}$ to be antisymmetric in $P$, which is what the last colormap checks for. Here, $B_{int}$ is calculated as $(\alpha_+ \rho_+ - \alpha_- \rho_- + G_+ n_+ - G_-n_-)/\mu_B$.

$\beta_\pm \neq 0$, $K_\pm \neq 0$, but with no dependence on $B_{ext}$ or $B_{int}$

Here are some examples of how the new parameters affect the energy splitting without doing any magnetic field dependent correction. Also, the simulation seems to break at some points for high values of the coefficients. Setting $\beta_+ = \beta_- = 0.1$, $K_+ = K_- = 0.01$: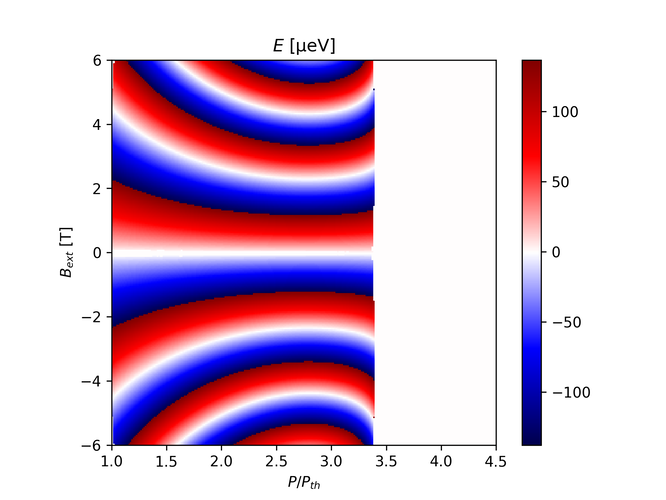

If we try setting $K_- = K_+ = 0$ with the same $\beta_\pm$: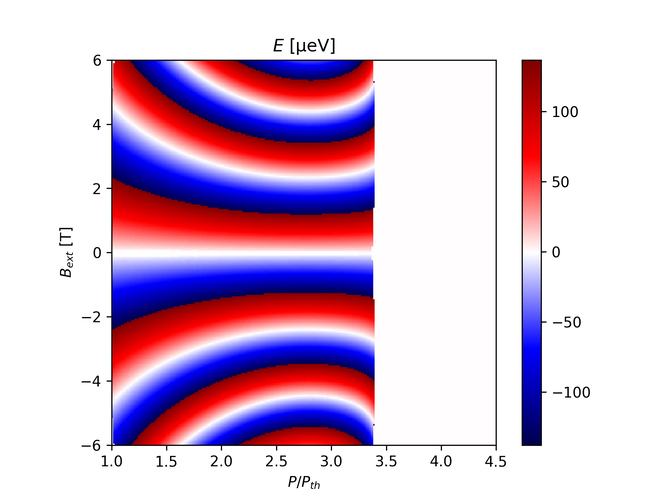

With $\beta_+ = \beta_- = 0.01$ and $K_- = K_- = 0$: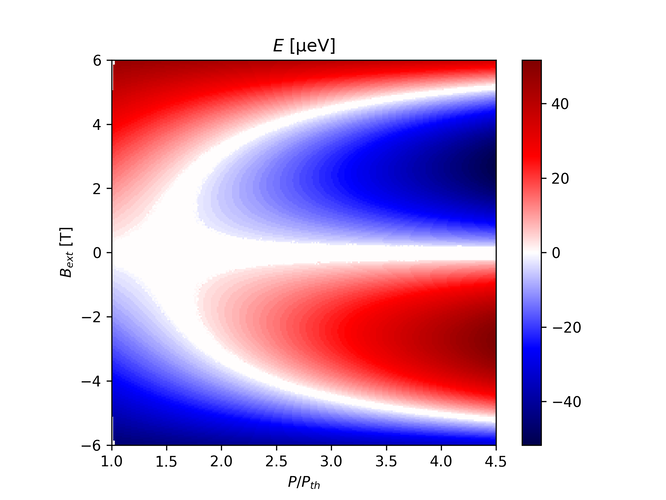

And with $K_- = K_+ = 1.0$ and $\beta_+ = \beta_- = 0.01$: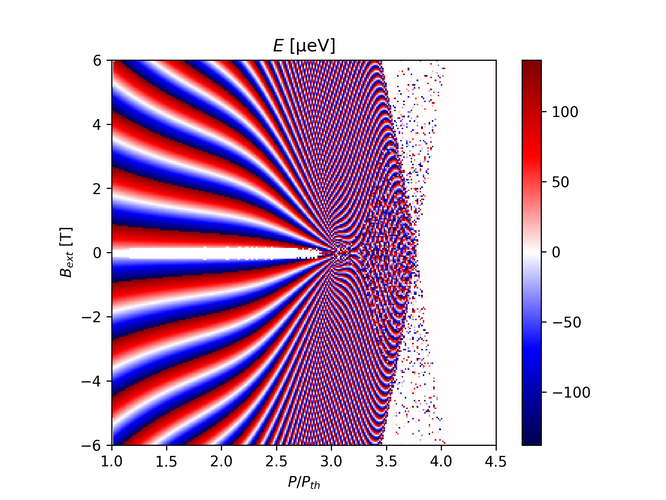

If we choose the $K_\pm = 0.01$ and try $\beta_+ = \beta_- = -0.01$: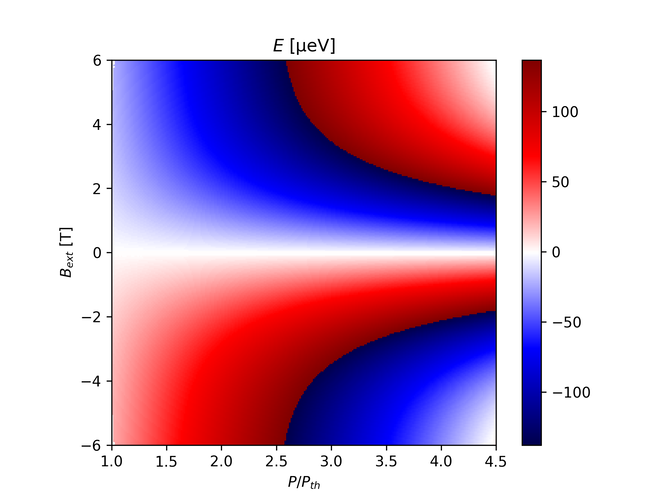

With $K_\pm = 0.001$ and $\beta_\pm = -0.001$: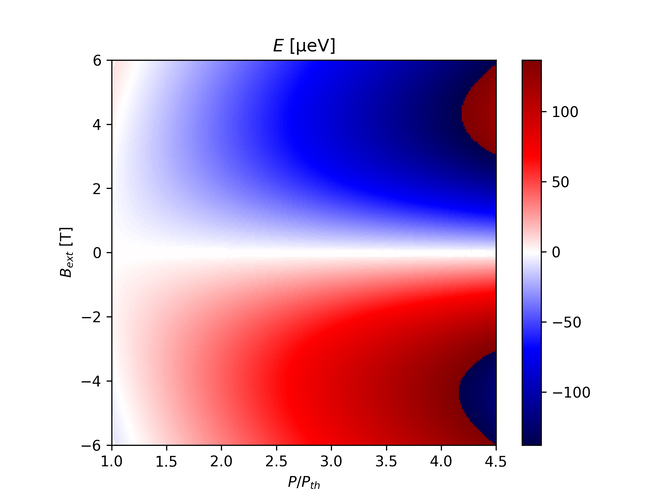

And with $K_\pm = 0.001$, $\beta_+ = 0.001$ and $\beta_- = -0.001$: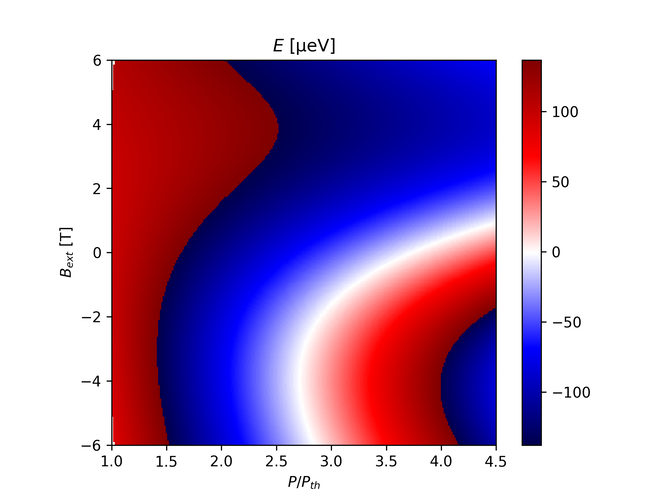

And to verify we get the same graph but reflected and with signs flipped if $\beta_+ = -0.001$ and $\beta_- = 0.001$: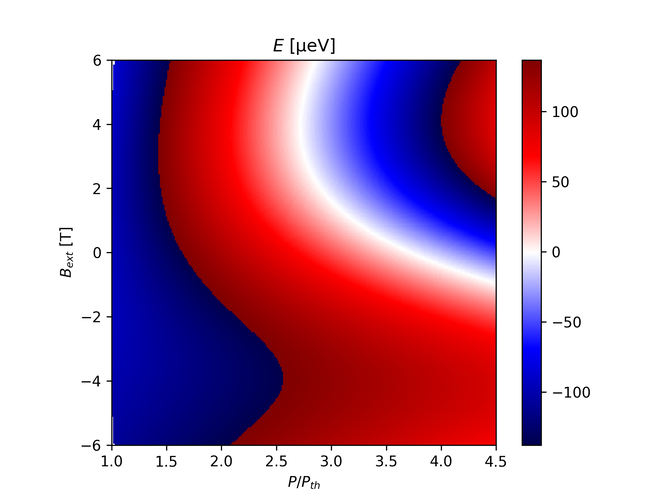

With $\beta_\pm$, $K_\pm$ and dependence on only $B_{ext}$

Here I'm going to define $\beta_{\pm,0} = 0.01$, $K_{\pm,0} = 0.001$ and obtain $\beta_\pm$ and $K_\pm$ from the following correction: $$ \{\beta,K\}_{\pm} = \{\beta,K\}_{\pm,0} \left(1 - \frac{\Delta}{(B_{ext} \mp B_0)^2 + \gamma_{res}^2}\right) $$

Starting from $\Delta = 0.5$, $B_0 = 3$ and $\gamma_{res} = 0.001$ so that we hopefully see a clear resonance. Here I'm going to push $P_0$ back a little bit because there some rather odd behavior at $B_{ext} = 0$.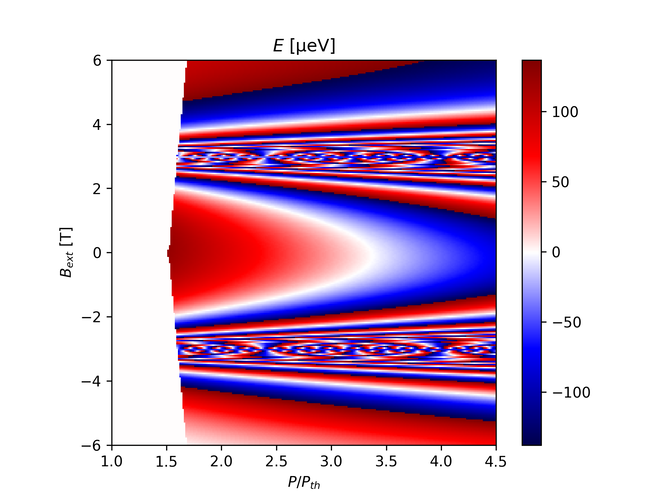

I suspect this is because of the width being too wide, so lets try setting it to $\Delta = 0.01$, and set $P_0$ back to 1.65.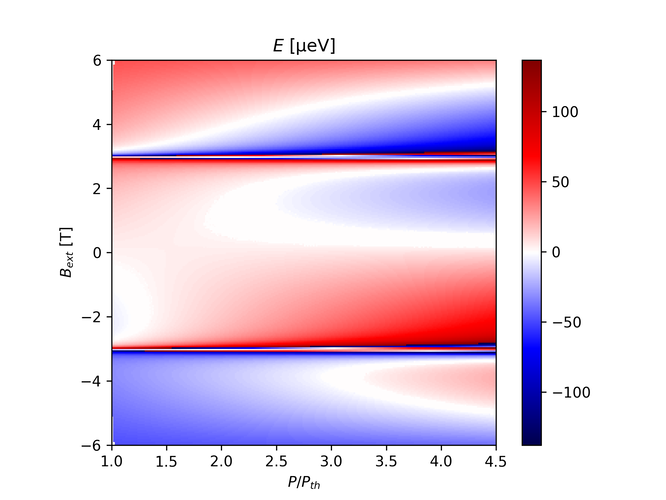

Now this looks somewhat unsymmetric, though this could be because of wraparound, so let's look at $B_{int}$: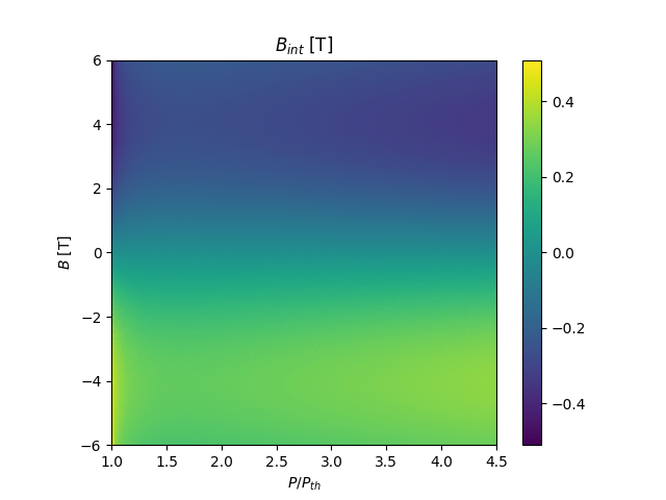

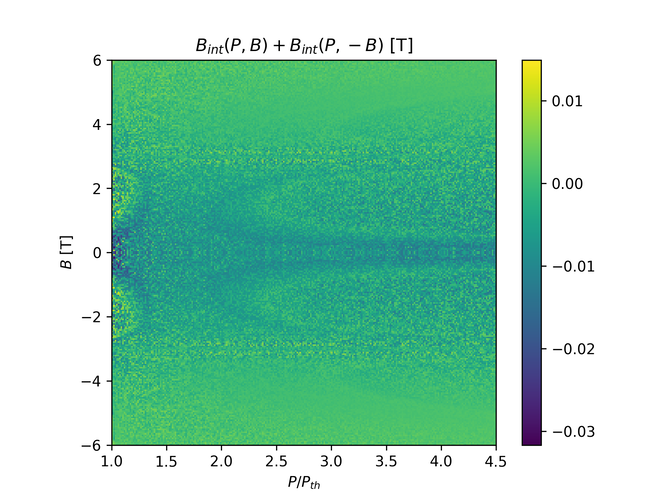
There seems to be slight asymmetry in the $B_{int}$ graph, however this is likely simply because of the actual range of $B_{int}$. In the code, $B_{ext}$ is in the range 6 T to -6 T, including 6 T but excluding -6 T. This means that the graph itself is in fact slightly asymmetric. To verify this is the problem, I'll try setting the range from and including -6 T up to and excluding 6 T, and we should see the error from total symmetry be skewed by the same amount in the opposite direction: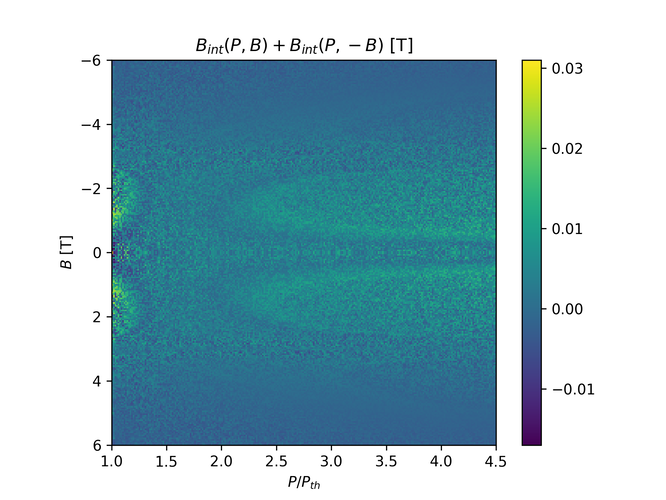

I believe this may go some way to answering why I'd been seeing an asymmetric $B_{int}$ in the more complicated simulation.

Next levels of complexity to try:

• making $\{\beta,K\}_\pm$ multiples of $\{\alpha,G\}_\pm$, without Feshbach correction.
• Add the Feshbach correction depending only on $B_{ext}$
• Make the correction depend on $B = B_{ext} + xB_{int}$ where $x$ is some amplifying factor.
• Correct $B_{int}$ so that it depends on $\{\beta,K\}_{\pm,0}$
• Correct $B_{int}$ so that it depends on $\{\beta,K\}_\pm$, using Newton's method to obtain approximations for the coefficients.