Kári's Research Blog
Stærri monotile grindur og fleiri penrose grindur.
Posted on

Table of Contents

Gröf

Í eftirfarandi myndum eru notaðar Gaussískar pumpur á forminu $P=p\exp\left(-\frac{(x-x_0)^2 + (y - y_0)^2}{\sigma^2}\right)$. Í eftirfarandi er $\sigma$= 1.2 µm, eða FWHM = 2.83 µm. Gildi sem eru notuð eru $\alpha$ = 0.01 µm$^2$, $\gamma_{LP}$ = 2 ps$^{-1}$, $\Gamma$ = 1 ps$^{-1}$, $R$ = 2 ps$^{-1}$µm$^{-2}$, $\eta$ = 1 ps$^{-1}$.

Monotile

Ég náði að búa til sæmilega stóra monotile grind með því að nota kóða frá Hastings Greer, tína út punktana og vista í NumPy skrá.

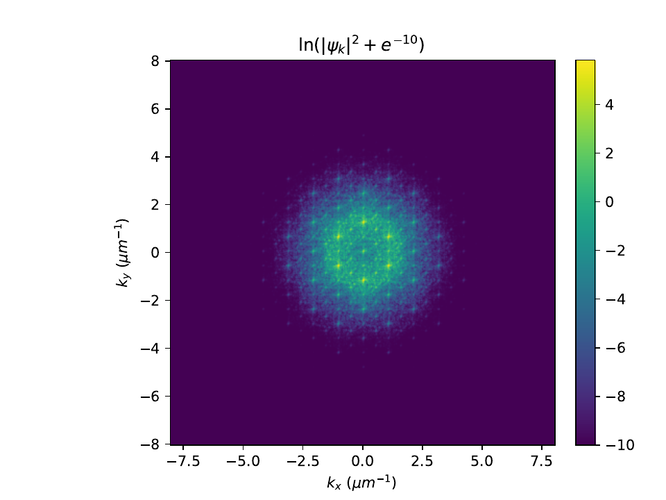
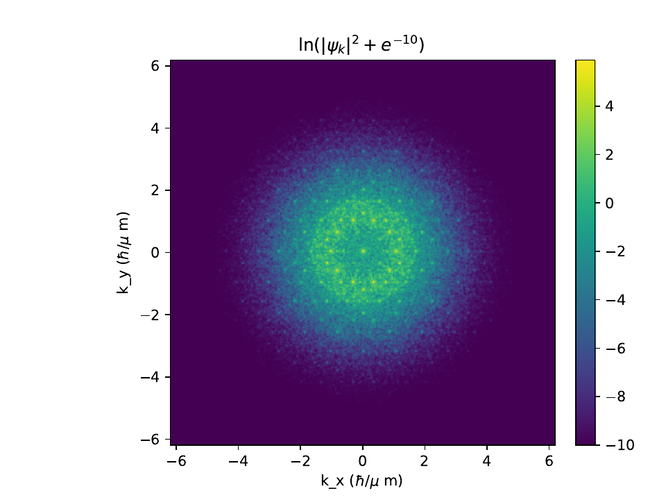
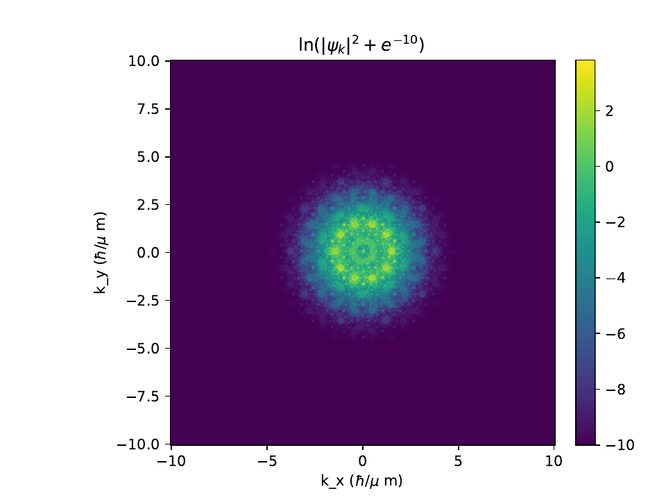
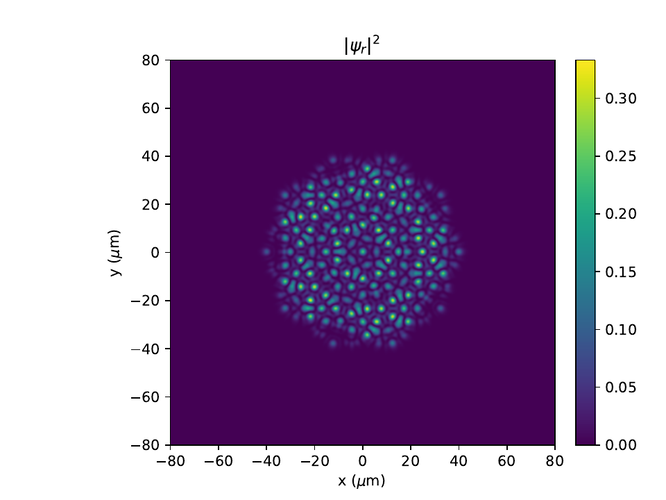
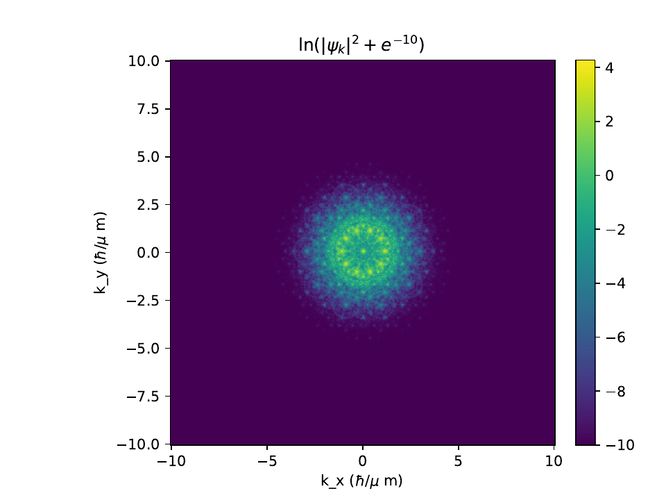
Hér eru r- og k-rúms myndir af $\psi$ í monotile grind. Til að sjá fínni smáatriði í rúminu er $e^{-10}$ bætt við algildið af $\psi$ í öðru og logrinn tekinn af niðurstöðunni.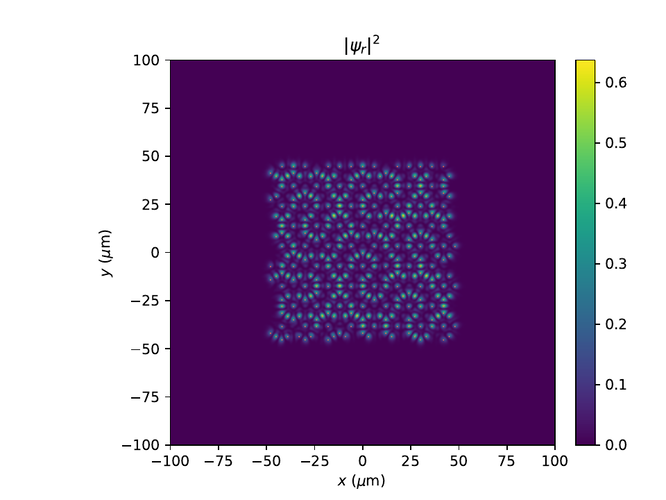

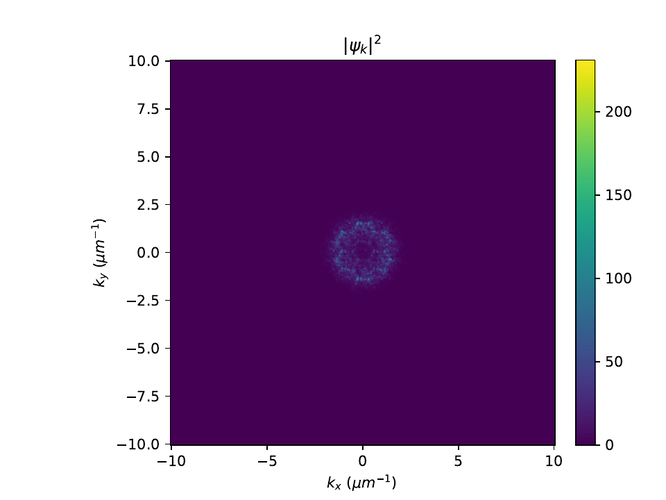
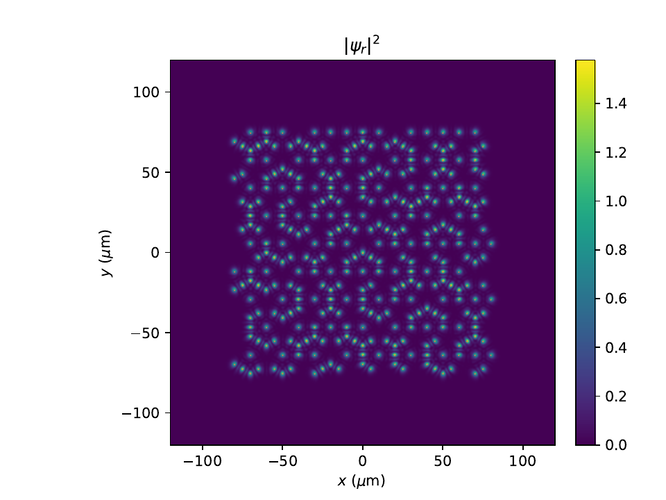
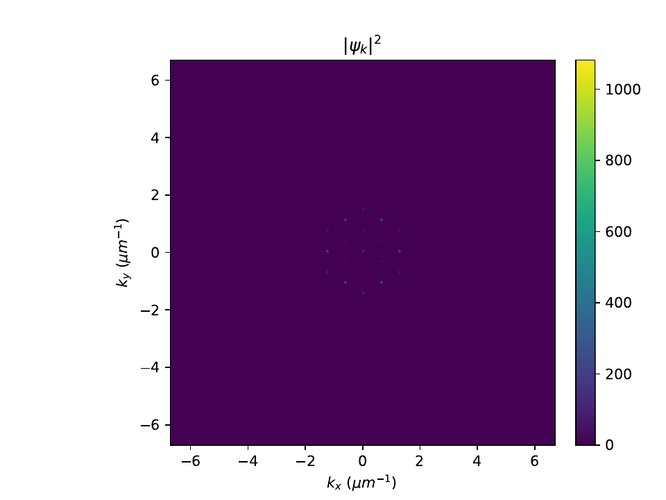
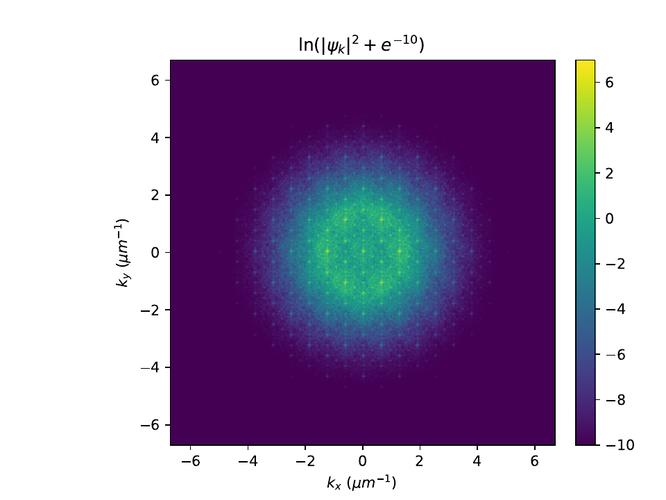
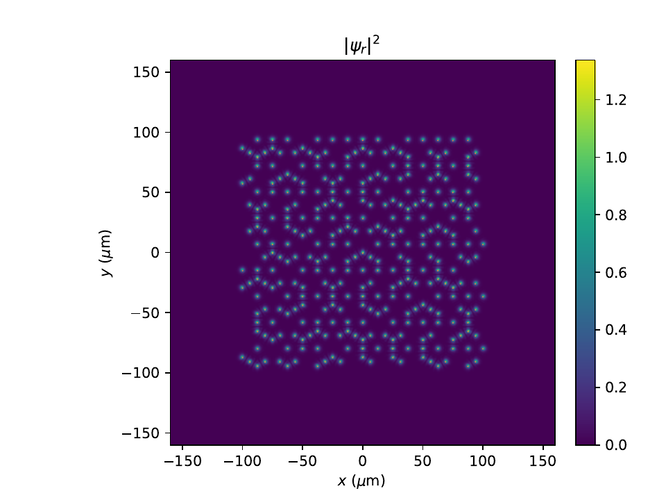
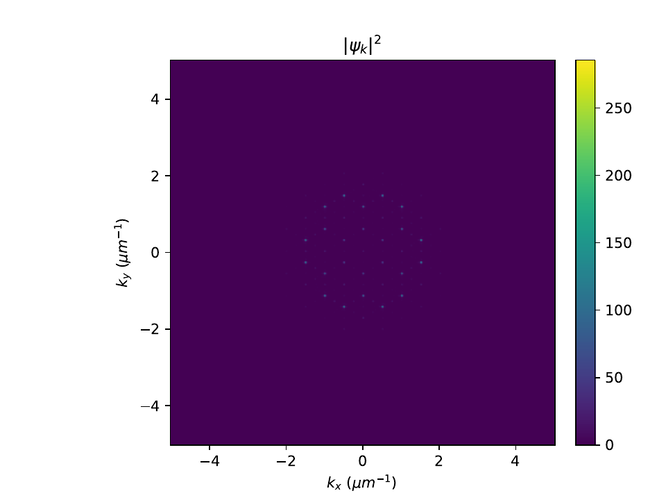
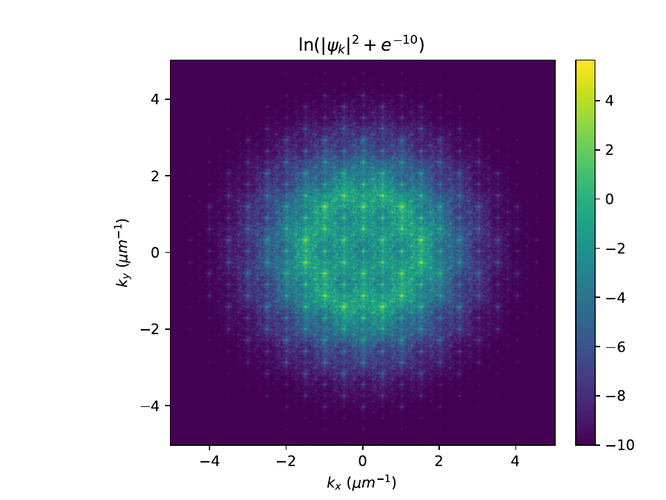
p=4 breidd ~100 µm, r-rúm
p=4, k-rúm, lograskali
p=4, k-rúm, sama mynd og að ofan með línulegum skala
p=10, r-rúm, breidd ~120 µm
p=10, k-rúm, línulegur skali
p=10, r-rúm, breidd ~160 µm
p=10, k-rúm, línulegur skali
p=10, k-rúm, lograskali
p=10, r-rúm, breidd ~210 µm
p=10, k-rúm, línulegur skali
p=10, k-rúm, lograskali

Penrose grind

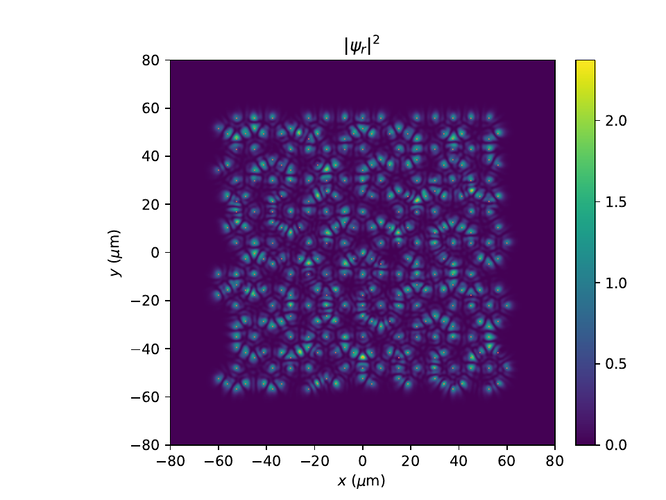
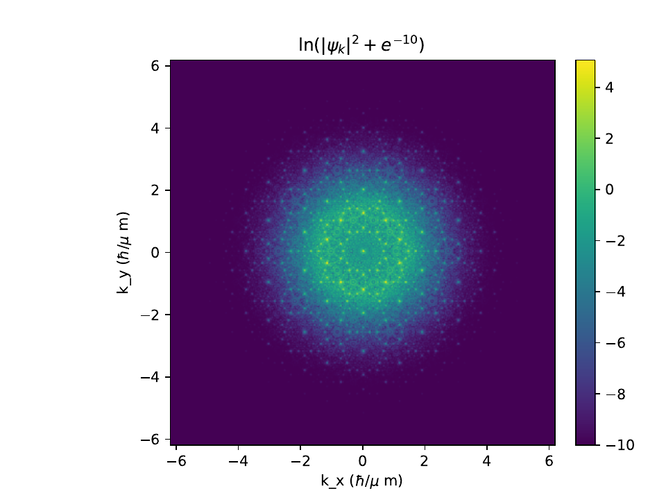
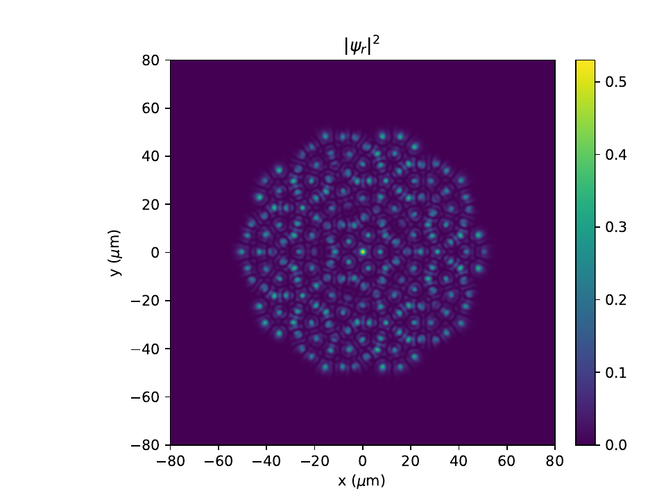
Eftirfarandi eru hermanir af Penrose grind með 5 skiptingum og mismunandi þvermálum, d.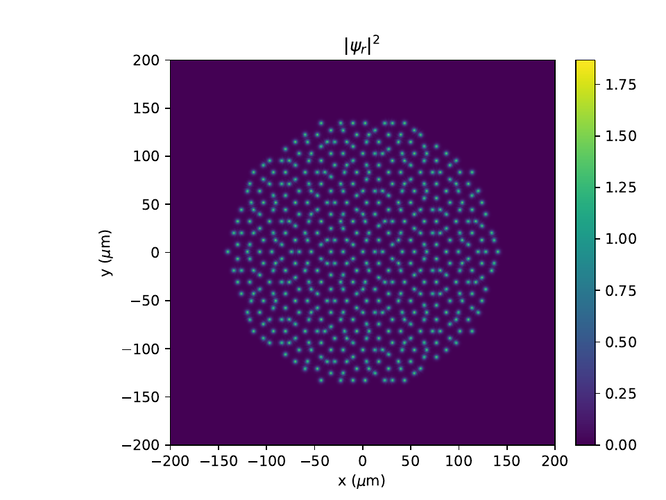

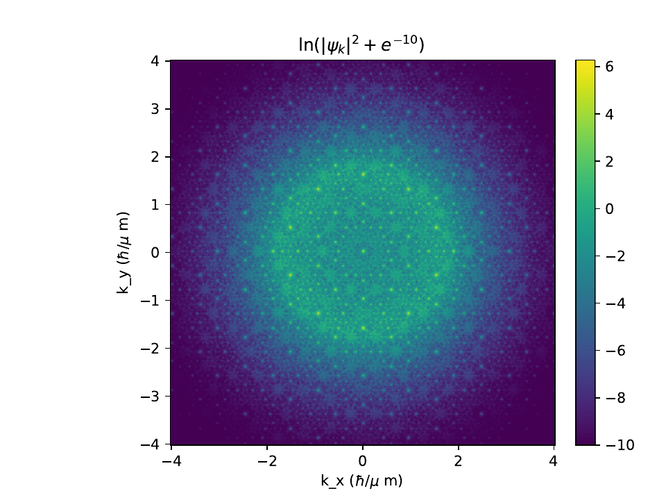
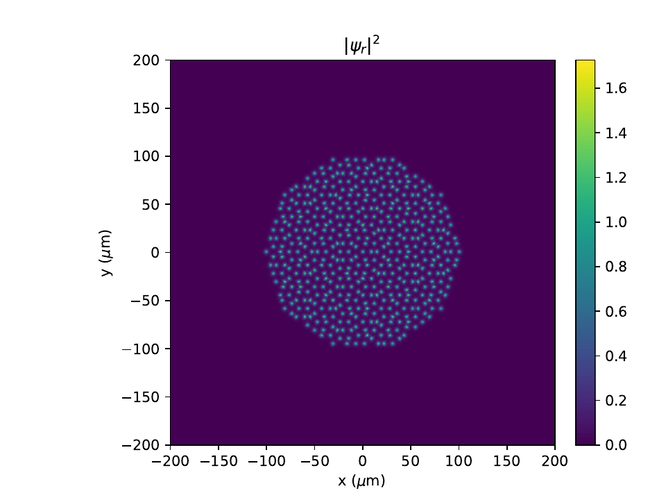
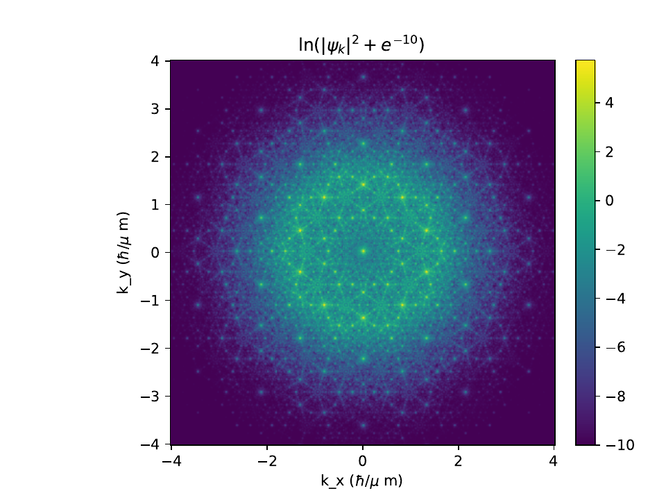
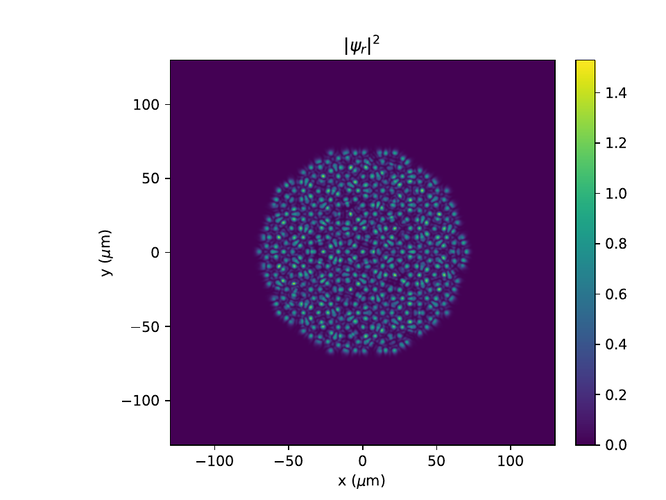
p = 16, d = 280 µm, r-rúm
p = 16, d = 280 µm, k-rúm lograskali
p = 12, d = 200 µm, r-rúm
p = 12, d = 200 µm, k-rúm lograskali
p = 8, d = 140 µm, r-rúm. Hér eru pumpurnar farnar að klessast upp við hverja aðra.
p = 8, d = 140 µm, k-rúm lograskali

Þar sem pumpurnar eru orðnar of þétt setnar minnkum við okkur í 4 skiptingar.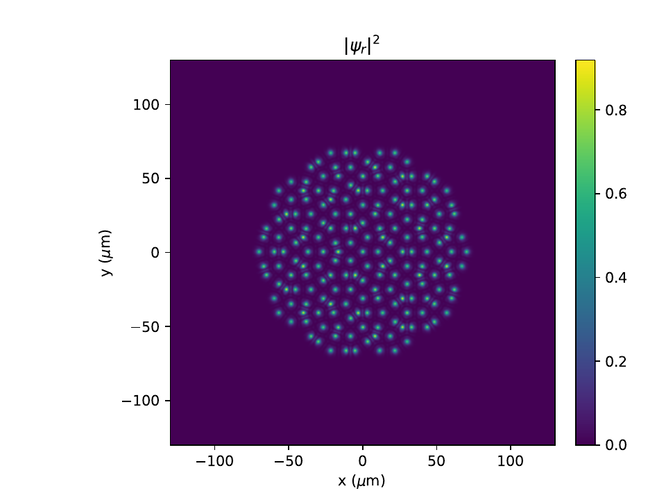

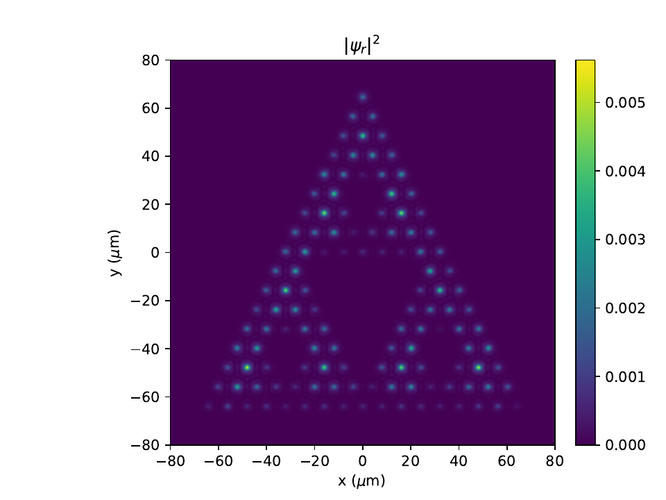
p = 8, d = 140 µm, r-rúm
p = 8, d = 140 µm, k-rúm lograskali
p = 5, d = 100 µm, r-rúm
p = 5, d = 100 µm, k-rúm lograskali
p = 4, d = 80 µm, r-rúm.
p = 4, d = 80 µm, k-rúm lograskali

Sierpinski grind

Til gamans prófaði ég að gera Sierpinski grind með hliðarlengdir 128 µm.

p = 4, d = 128 µm