A distance scan

The above video presents a continuous distance scan of a system of three trapped condensates in an equilateral triangular configuration. The left is is the intensity squared of the order parameter in r-space, on the right is its phase map (specifically the phase difference relative to an arbitrarily chosen point so that the animation doesn't give anyone a seizure). The arrows on the phase map indicate the direction of the probability current, but not the magnitude. Each condensate starts at a distance d=12.2 µm from the origin and is slowly moved to d=19 µm. There are some interesting features in this scan.

Firstly, close to the end of the simulation the condensates have locked phases so that there is approximately a $2\pi/3$ phase difference between each one. This is a common feature of vortex states which have been observed in systems of untrapped condensates but have not been observed between coupled traps. Another interesting feature of this state is that the condensates are "$\pi$-bonded" in this configuration, i.e. configured in a $\Delta$ rather than a Y.

Secondly, though this may be somewhat outside the scope we've been looking at, is the appearance of a secondary lobe in the part of each trap closer to the other condensates (at 6-8 seconds). I'm not sure what could be the theoretical explanation for this lobe, perhaps something to do with standing waves and some kind of interference. It doesn't seem to be simply a result of the optical pumps being smooshed together, as the lobe appears as the condensates travel further away from each other and reaches its greatest intensity at the 8 second mark.

Next is to check whether these features arise with static pumping, or if these are transient or dynamic phenomena. I think that there's a distinction to be made here between transient and dynamic, or perhaps assisted. A transient behaviour is inherently short lived, while a general dynamically induced state may also be metastable; strongly metastable, even. As the vortex state appeared at around 19 µm separation I checked with static pumping with d between 17 µm and 22 µm. I have somewhat looked into the secondary lobe state. I have thus far been unable to produce it, but I may be able to by fine tuning d and the pump strength.

The vortex state

I found two quite interesting states w.r.t vorticity. A system with d = 22 µm apparently doesn't show this 2$\pi$ phase difference, and is also in a Y-configuration: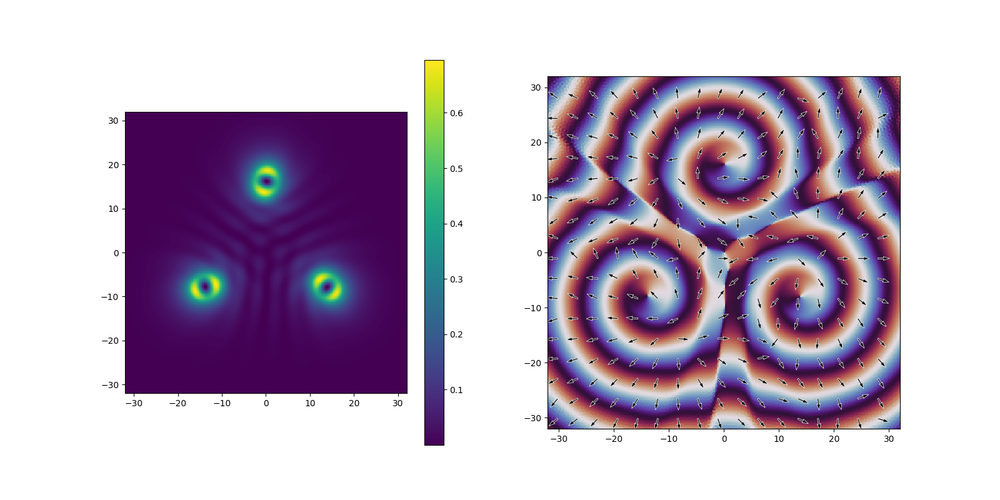

This state does, however display one feature of symmetric vortex states, which is destructive interference at the origin. I also created an animation to ensure this is really a steady state, and indeed it was, so I omitted it from this post. However, finding the indices of the array that correspond most closely with the centers of the traps and taking the phase difference between them yields the following plot: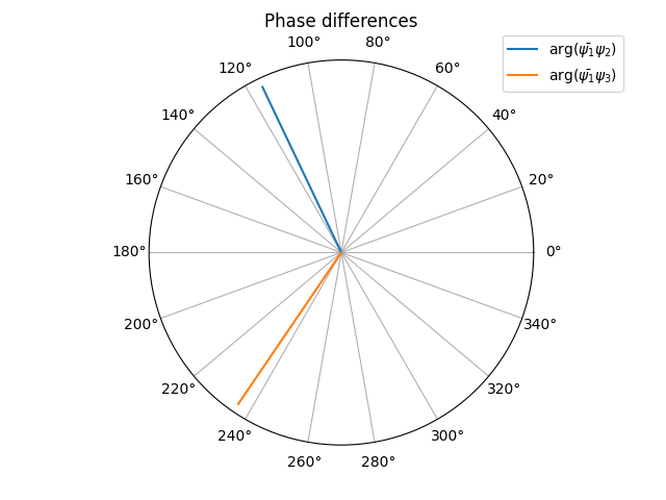

The curves appear to be straight lines, but that is just how robust the synchronization between them is. Which is what one should expect in a vortex state. As I understand, though, this phase difference should apply if you compare any arbitrary point in a condensate with a corresponding point in the other condensates. With this line of thinking, I simply chose points that are slightly nudged from the center and obtained this graph: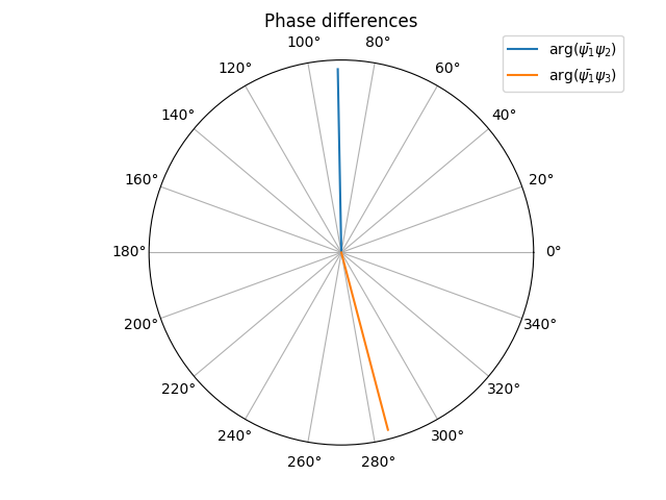

Which displays quite a different behaviour that is still different from what's apparent on the snapshot. However, seeing as the snapshot gives us a view of the entire condensate it should be more reliable than either of the other indicators. One flaw of my approach here may be that the centers of each condensate might not correspond entirely to the centers of the pump profiles, since repulsive forces from the other condensates may nudge the real center of mass of each condensate away from the origin.

At d = 20 µm, we sort of obtain a $2\pi/3$ angular, though not phase difference between the condensates.

There are three quite interesting features of this state. One is that it seems to be quite weakly stable; even though this simulation ran for just as long as the one at 22 µm there are still visible oscillations in the phase map and even subtle ones in the intensity map. Another interesting feature is that there is now constructive interference at the origin, which is the opposite of what's expected in vortex states.

The third interesting thing is that the phase structure in each condensate is qualitatively different from the one at 22 µm. Rather than varying smoothly around the center, there are two blobs, each with diametrically opposite phases, and the blobs are aligned so that they are facing the same phase blobs in the other condensates. The sharp discontinuity in phase could explain why the state is so weakly stable.

I have also run the simulation at d = 17 - 19 µm, but this variously give non-steady state, though apparently cyclical, results or doesn't observe the $2\pi/3$ phase-difference locking.